Difference between revisions of "Schrodinger equation"
(username removed) (Tidy up) |
(username removed) (Added section on time-independent equation and on one of the examples) |
||
| Line 8: | Line 8: | ||
<math>i\hbar\frac{\partial}{\partial t}|\Psi\rangle=\hat H|\Psi\rangle</math> | <math>i\hbar\frac{\partial}{\partial t}|\Psi\rangle=\hat H|\Psi\rangle</math> | ||
| − | where <math>i</math> is the [[complex number|imaginary unit]] | + | where |
| + | :<math>i</math> is the [[complex number|imaginary unit]] | ||
| + | :<math>\hbar</math> is the [[Planck's constant|reduced Planck's constant]] | ||
| + | :<math>|\Psi\rangle</math> is the quantum mechanical state or wavefunction (expressed here in [[Dirac notation]]) | ||
| + | :<math>\hat H</math> is the [[Hamiltonian]] operator. | ||
The left side of the equation describes how the wavefunction changes with time; the right side is related to its energy. For the simplest case of a particle of mass m moving in a one-dimensional potential V(x), the Schrodinger equation can be written | The left side of the equation describes how the wavefunction changes with time; the right side is related to its energy. For the simplest case of a particle of mass m moving in a one-dimensional potential V(x), the Schrodinger equation can be written | ||
| Line 16: | Line 20: | ||
</math> | </math> | ||
| − | + | This can be expanded to give the three dimensional time dependent Schrodinger equation using the [[Laplacian|Laplacian operator]], <math>\nabla^2</math>: | |
| + | |||
| + | <math> | ||
| + | -\frac{\hbar^2}{2m} | ||
| + | \nabla^2 \Psi | ||
| + | +V(x)\Psi=i\hbar\frac{\partial \Psi}{\partial t} | ||
| + | </math> | ||
| + | |||
| + | In this case, the wavefunction is <math>\Psi(x,y,z,t)</math>. | ||
===Derivation=== | ===Derivation=== | ||
| Line 35: | Line 47: | ||
from which Schrodinger's equation and the eigenvalue problem <math> \hat H\Psi = E\Psi</math> can be easily seen. | from which Schrodinger's equation and the eigenvalue problem <math> \hat H\Psi = E\Psi</math> can be easily seen. | ||
| + | |||
| + | ===Time-independent Schrodinger Equation=== | ||
| + | |||
| + | The wavefunction is a multi-variable function, that is to say it depends on both [[time]] and space. Suppose that we have a function only in terms of space, <math>\psi(x)</math>. We can write the full wavefunction as <math>\Psi(x,t) = \psi(x) e^{-iEt/ \hbar}</math> for a state of definite energy. This type of state is also know as a "stationary state" as the probability distribution for this type of wavefunction over time is constant (see below). Substituting this wavefunction into the Schrodinger equation: | ||
| + | |||
| + | <math>- \frac{\hbar^2}{2m} \frac{\partial^2 \psi(x)}{\partial x^2} e^{-iEt/ \hbar} + V(x) \psi(x) e^{-iEt/ \hbar} = E \psi(x) e^{-iEt/ \hbar} </math> | ||
| + | |||
| + | Cancelling the factor of <math>e^{-iEt/ \hbar}</math> results in a [[differential equation]] that only depends on <math>x</math>. This is the '''time-independent Schrodinger equation''': | ||
| + | |||
| + | <math>- \frac{\hbar^2}{2m} \frac{d^2 \psi(x)}{dx^2} + V(x) \psi(x) = E \psi(x)</math> | ||
| + | |||
| + | <math>\psi(x)</math> is often called the "wavefunction", though strictly speaking it is <math>\Psi(x,t)</math> that is the wavefunction. | ||
| + | |||
| + | ===Solutions to the Schrodinger Equation=== | ||
| + | |||
| + | Solutions to the Schrodinger equation are known as "wavefunctions". However, for a solution to be physically valid, two conditions must be imposed on these solutions. These are that both the wavefunction and its first derivative must be [[Continuous function|continuous]]. Wavefunctions may be [[Real number|real]] or [[Complex numbers|complex]]. | ||
| + | |||
| + | Since the Schrodinger equation is [[Linear equations|linear]], if <math>\psi_1 (x)</math> and <math>\psi_2 (x)</math> are solutions, then <math>\psi_1 (x) + \psi_2 (x)</math> is also a solution. | ||
===Eigenvalue problems=== | ===Eigenvalue problems=== | ||
| Line 46: | Line 76: | ||
===Interpretation of the Wavefunction=== | ===Interpretation of the Wavefunction=== | ||
| − | The wavefunction is related to the probability of observing a particle at that location in space. More specifically, where the wavefunction has a greater value of <math>|\Psi|^2</math> at one location, a, compared to another, b, then the particle is more likely to be observed at a than b. | + | The wavefunction is related to the probability of observing a particle at that location in space. More specifically, where the wavefunction has a greater value of <math>|\Psi|^2</math> at one location, a, compared to another, b, then the particle is more likely to be observed at a than b. Note that the [[Absolute value|modulus] must be taken since the wavefunction may be [[Complex numbers|complex. |
====Normalisation==== | ====Normalisation==== | ||
| Line 64: | Line 94: | ||
For some wavefunctions, such as that of a free particle, the integral above does not exist and so they are said to be non-normalisable. | For some wavefunctions, such as that of a free particle, the integral above does not exist and so they are said to be non-normalisable. | ||
| − | ==Examples for the | + | ==Examples for the Time-Independent Equation== |
===Free particle in one dimension=== | ===Free particle in one dimension=== | ||
| − | In this case, <math>V(x)=0</math> | + | In this case, <math>V(x)=0</math>, the time-independent Schrodinger equation is: |
| + | |||
| + | <math>\frac{d^2 \psi}{dx^2} = - \frac{2mE}{\hbar^2} \psi</math> | ||
| + | |||
| + | In this case, the solution is sinusoidal for some constants, <math>A</math>, <math>B</math>, <math>C</math>, and <math>D</math>: | ||
| − | <math>\psi= | + | <math>\psi=A \sin{kx} + B \cos{kx} = Ce^{ikx} + De^{-ikx}</math> |
| − | + | The [[energy]] can then be found as: | |
<math>E=\frac{\hbar^2 k^2}{2m}</math> | <math>E=\frac{\hbar^2 k^2}{2m}</math> | ||
| − | Physically, this corresponds to a wave travelling with a [[momentum]] given by <math>\hbar k</math>, where k can in principle take any value. | + | Physically, this corresponds to a wave travelling with a [[momentum]] given by <math>\hbar k</math>, where k can in principle take any value. This wavefunction is not normalisable. |
===Particle in a box=== | ===Particle in a box=== | ||
Consider a one-dimensional box of width a, where the potential energy is 0 inside the box and infinite outside of it. We can describe this potential by: | Consider a one-dimensional box of width a, where the potential energy is 0 inside the box and infinite outside of it. We can describe this potential by: | ||
| − | <math> | + | <math>V(x) = |
\begin{cases} | \begin{cases} | ||
\infty &\quad\text{if } x < 0\\ | \infty &\quad\text{if } x < 0\\ | ||
| Line 125: | Line 159: | ||
You may wonder what happens about the constant <math>B</math>. Since the Schrodinger equation is linear, <math>B</math> can take any value and the resulting wavefunction would be a solution. Since <math>|\psi (x)|^2</math> represents the probability of finding the particle at position <math>x</math> and across all space, this probability must equal 1, we can solve for <math>B</math>. We do this by integrating <math>|\psi (x)|^2</math> from <math>-\infty</math> to <math> + \infty</math>. Therefore the full solution is: | You may wonder what happens about the constant <math>B</math>. Since the Schrodinger equation is linear, <math>B</math> can take any value and the resulting wavefunction would be a solution. Since <math>|\psi (x)|^2</math> represents the probability of finding the particle at position <math>x</math> and across all space, this probability must equal 1, we can solve for <math>B</math>. We do this by integrating <math>|\psi (x)|^2</math> from <math>-\infty</math> to <math> + \infty</math>. Therefore the full solution is: | ||
| − | <math> | + | <math>V(x) = |
\begin{cases} | \begin{cases} | ||
\sqrt{\frac{2}{a}} \sin{\omega x} &\quad\text{if } x < 0\\ | \sqrt{\frac{2}{a}} \sin{\omega x} &\quad\text{if } x < 0\\ | ||
Revision as of 18:32, September 20, 2016
The Schrodinger equation is a linear differential equation used in various fields of physics to describe the time evolution of quantum states. It is the fundamental equation of non-relativistic quantum meachincs. The equation is named after its discoverer, Erwin Schrodinger.
Mathematical forms
General time-dependent form
The Schrodinger equation may generally be written
where
is the imaginary unit
is the reduced Planck's constant
is the quantum mechanical state or wavefunction (expressed here in Dirac notation)
is the Hamiltonian operator.
The left side of the equation describes how the wavefunction changes with time; the right side is related to its energy. For the simplest case of a particle of mass m moving in a one-dimensional potential V(x), the Schrodinger equation can be written
This can be expanded to give the three dimensional time dependent Schrodinger equation using the Laplacian operator, 
:
In this case, the wavefunction is 
.
Derivation
The quickest and easiest way to derive Schrodinger's equation is to understand the Hamiltonian operator in quantum mechanics. In classical mechanics, the total energy of a system is given by
where p is the momentum of the particle and V(x) is its potential energy. Applying the quantum mechanical operator for momentum:
and subbing into the classical mechanical form for energy, we get the same Hamiltonian operator in quantum mechanics:
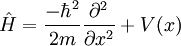
from which Schrodinger's equation and the eigenvalue problem 
can be easily seen.
Time-independent Schrodinger Equation
The wavefunction is a multi-variable function, that is to say it depends on both time and space. Suppose that we have a function only in terms of space, 
. We can write the full wavefunction as 
for a state of definite energy. This type of state is also know as a "stationary state" as the probability distribution for this type of wavefunction over time is constant (see below). Substituting this wavefunction into the Schrodinger equation:
Cancelling the factor of 
results in a differential equation that only depends on 
. This is the time-independent Schrodinger equation:
is often called the "wavefunction", though strictly speaking it is 
that is the wavefunction.
Solutions to the Schrodinger Equation
Solutions to the Schrodinger equation are known as "wavefunctions". However, for a solution to be physically valid, two conditions must be imposed on these solutions. These are that both the wavefunction and its first derivative must be continuous. Wavefunctions may be real or complex.
Since the Schrodinger equation is linear, if 
and 
are solutions, then 
is also a solution.
Eigenvalue problems
In many instances, steady-state solutions to the equation are of great interest. Physically, these solutions correspond to situations in which the wavefunction has a well-defined energy. The energy is then said to be an eigenvalue for the equation, and the wavefunction corresponding to that energy is called an eigenfunction or eigenstate. In such cases, the Schrodinger equation is time-independent and is often written
Here, E is energy, H is once again the Hamiltonian operator, and 
is the energy eigenstate for E.
One example of this type of eigenvalue problem is an electrons bound inside an atom.
Interpretation of the Wavefunction
The wavefunction is related to the probability of observing a particle at that location in space. More specifically, where the wavefunction has a greater value of 
at one location, a, compared to another, b, then the particle is more likely to be observed at a than b. Note that the [[Absolute value|modulus] must be taken since the wavefunction may be [[Complex numbers|complex.
Normalisation
Wavefunctions are said to be "normalisable" if the following integral exists:
If that integral exists, then the wave function may be normalised by introducing a constant, 
, such that
Note that may be complex. This will produce and new wavefunction, 
, which has the property that:
This is the probability of observing the particle between points a and b. For some wavefunctions, such as that of a free particle, the integral above does not exist and so they are said to be non-normalisable.
Examples for the Time-Independent Equation
Free particle in one dimension
In this case, 
, the time-independent Schrodinger equation is:
In this case, the solution is sinusoidal for some constants, 
, 
, 
, and 
:
The energy can then be found as:
Physically, this corresponds to a wave travelling with a momentum given by 
, where k can in principle take any value. This wavefunction is not normalisable.
Particle in a box
Consider a one-dimensional box of width a, where the potential energy is 0 inside the box and infinite outside of it. We can describe this potential by:
This is also known as "the infinite square well".
This means that must be zero outside the box. One can verify (by substituting into the Schrodinger equation) that
is a solution if 
where n is any integer. Thus, rather than the continuum of solutions for the free particle, for the particle in a box there is a set of discrete solutions with energies given by
Derivation
The particle cannot exits outside the box where the potential is infinite. Hence the wavefunction, , here must be zero outside the box. Now let us consider inside the box. The Schrodinger equation inside the potential well becomes:
Rearranging this equation give
This has the same form as the basic equation for simple harmonic motion. Hence we can give the solution as
where and are unknown constants and 
is equal to 
. To ind the value of the the constants, we substitute in boundary conditions. An additional constraint is that wavefunctions must be continious (they cannot suddenly change value). Hence
From this we can see that must be zero. Using the continuous constraint again, we see that
The continuous constraint is only satisfied when 
where 
is an integer. We also note that 
is not a solution as the wavefunction would be zero everywhere and so the probability of finding the particle is 0. We also discard solutions for 
since these are not "new" solutions. As 
, these are just the negative of solutions with positive . By setting , we can find the energy 
as:
And so:
You may wonder what happens about the constant . Since the Schrodinger equation is linear, can take any value and the resulting wavefunction would be a solution. Since 
represents the probability of finding the particle at position and across all space, this probability must equal 1, we can solve for . We do this by integrating from 
to 
. Therefore the full solution is:
where is as above.
Relativity
The Schrodinger equation is non-relativistic in nature. It can be re-derived taking special relativity into account. This results in the Klein-Gordon equation.
