Difference between revisions of "Series (mathematics)"
m (→Infinite series) |
DavidB4-bot (Talk | contribs) (→Convergence: Spelling/Grammar Check, typos fixed: However → However,) |
||
| (24 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| − | In mathematics a '''series''' is the sum of a [[sequence]] of numbers. | + | In mathematics a '''series''' is the sum of a [[sequence]] of numbers. This article is intended to give the reader some understanding on the summation of finite series and why some infinite series converge whilst others diverge. |
==Summation notation== | ==Summation notation== | ||
| − | |||
If ever value in a sequence is denoted <math>a_{n}</math>, then the sum of ''N'' of these are denoted, | If ever value in a sequence is denoted <math>a_{n}</math>, then the sum of ''N'' of these are denoted, | ||
<math>a_{1}+a_{2}+a_{3}+\dots+a_{N}=\sum^{N}_{n=1}a_{n}</math> | <math>a_{1}+a_{2}+a_{3}+\dots+a_{N}=\sum^{N}_{n=1}a_{n}</math> | ||
| − | This is | + | This is usually pronounced "the sum of 1 to N of a n" (note that this is still an ambiguous statement which is why mathematics is more rigorous written down). |
| − | If we are | + | If we are concerned with particular number we can move the starting index. For example, |
<math>\sum_{n=500}^{1000}n</math> | <math>\sum_{n=500}^{1000}n</math> | ||
| − | is the sum of the | + | is the sum of the integers from 500 to 1000. |
==Finite series== | ==Finite series== | ||
| + | ''For more detail see [[Finite series]].'' | ||
| − | The sum of finite series is | + | The sum of finite series is in general relatively straight forward to calculate it consist of merely summing together all the numbers in a sequences. However this can be time consuming and in pre-computer mathematics many shortcuts were found. |
| − | Gauss once famously was given the assignment by his teacher to add the number between 1 and 100. The rest of the students were working hard | + | Gauss once famously was given the assignment by his teacher to add the number between 1 and 100. The rest of the students were working hard adding carefully, but after less than a minute he correctly wrote 5050. This story whilst is allegorical leads to a key insight in finite sums, |
| − | <math>\sum^{N}_{n=1}n=\frac{N(N+1)}{2}</math> | + | :<math>\sum^{N}_{n=1}n=\frac{N(N+1)}{2}</math> |
==Infinite series== | ==Infinite series== | ||
| − | + | ''For more detail see [[Infinite series]].'' | |
| − | + | The idea that an infinite number of additions lead to a finite number was initial seen as problematic or even impossible, (see [[Zeno's paradox]]). However it is straightforward to see why this could happen, | |
| − | <math>S=\ | + | :Let <math>S=\sum^{\infty}_{n=1}\frac{1}{2^{n}}</math> |
| − | <math> | + | :<math>S=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\dots</math> |
| − | <math>2S=1+ | + | :<math>2S=1+\frac{1}{2}+\frac{1}{4}+\dots</math> |
| − | <math> | + | :<math>2S=1+S</math> |
| − | This | + | :<math>S=1</math> |
| + | |||
| + | This one of an important class of infinites series called the geometric series. | ||
===Geometric series=== | ===Geometric series=== | ||
| Line 45: | Line 47: | ||
===Convergence=== | ===Convergence=== | ||
| − | However all | + | ''For more detail see [[Convergence]]'' |
| + | |||
| + | However all infinite series don't converge, a famous example is, | ||
| + | |||
| + | :<math>\sum^{\infty}_{n}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\dots</math> | ||
| + | |||
| + | :<math>\geq 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\dots</math> | ||
| + | |||
| + | :<math>=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\dots</math> | ||
| + | |||
| + | Adding together an infinite string of halves will not give you a finite number so this sequence is said to '''diverge'''. | ||
| + | |||
| + | A series will only converge if <math>\lim_{n\rightarrow\infty}a_{n}=0</math>. However, there are two other conditions for real series, | ||
| + | |||
| + | ====Power Series convergence==== | ||
| + | |||
| + | A power series is of the form, | ||
| + | |||
| + | :<math>\sum^{\infty}_{n=1}a_{n}=\sum^{\infty}_{n=1}b_{n}(x-a)^{n}</math>, | ||
| + | |||
| + | This will converge if <math>\lim_{n\rightarrow\infty}|\frac{a_{n+1}}{a_{n}}|<1</math>. | ||
| − | + | ====Alternating Series convergence==== | |
| − | + | An alternating series is of the form, | |
| − | <math> | + | :<math>\sum^{\infty}_{n=1}(-1)^{n}a_{n}</math> |
| − | + | This will converge if <math>0\leq a_{n+1}<a_{n}</math>. | |
==Usage== | ==Usage== | ||
| + | *[[Integral]] | ||
| + | *[[Riemann Zeta function]] | ||
| + | *[[Taylor series]] | ||
| + | *[[Fourier series]] | ||
| − | [[Category: | + | [[Category:Mathematics]] |
Latest revision as of 13:46, August 22, 2016
In mathematics a series is the sum of a sequence of numbers. This article is intended to give the reader some understanding on the summation of finite series and why some infinite series converge whilst others diverge.
Contents
Summation notation
If ever value in a sequence is denoted 
, then the sum of N of these are denoted,
This is usually pronounced "the sum of 1 to N of a n" (note that this is still an ambiguous statement which is why mathematics is more rigorous written down).
If we are concerned with particular number we can move the starting index. For example,
is the sum of the integers from 500 to 1000.
Finite series
For more detail see Finite series.
The sum of finite series is in general relatively straight forward to calculate it consist of merely summing together all the numbers in a sequences. However this can be time consuming and in pre-computer mathematics many shortcuts were found.
Gauss once famously was given the assignment by his teacher to add the number between 1 and 100. The rest of the students were working hard adding carefully, but after less than a minute he correctly wrote 5050. This story whilst is allegorical leads to a key insight in finite sums,
Infinite series
For more detail see Infinite series.
The idea that an infinite number of additions lead to a finite number was initial seen as problematic or even impossible, (see Zeno's paradox). However it is straightforward to see why this could happen,
- Let
This one of an important class of infinites series called the geometric series.
Geometric series
Where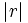 
denotes the absolute value of r.
Convergence
For more detail see Convergence
However all infinite series don't converge, a famous example is,
Adding together an infinite string of halves will not give you a finite number so this sequence is said to diverge.
A series will only converge if 
. However, there are two other conditions for real series,
Power Series convergence
A power series is of the form,
,
This will converge if 
.
Alternating Series convergence
An alternating series is of the form,
This will converge if 
.
