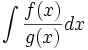Difference between revisions of "Methods of integration"

From Conservapedia
Jump to: navigation, search
(Added a section on the reverse chain rule)
m (Reverted edits by BertJonson64 (talk) to last revision by FredericBernard)
 
(5 intermediate revisions by 3 users not shown)
Line 37: Line 37:
 
Given an integral  
 
Given an integral  
  
−
:<big><math>\int\frac{2x}{x^2+3}dx</math></big>
+
:<math>\int\frac{2x}{x^2+3}dx</math>
  
−
We can substitute the term :<big><math>x^2+3</math></big> with a u.  Giving us
+
We can substitute the term ''x''<sup>2</sup>+3 with a ''u''.  Giving us
  
−
:<big><math>u=x^2+3</math></big>
+
:<math>u=x^2+3</math>
  
−
We then take the derivative of u with respect to x,
+
We then take the derivative of ''u'' with respect to ''x'',
  
−
:<big><math>\frac{du}{dx}=2x</math></big>
+
:<math>\frac{du}{dx}=2x</math>
  
−
We then set the terms equal to du,
+
We then set the terms equal to d''u'',
  
−
:<big><math>du=2xdx</math></big>
+
:<math>du=2xdx</math>
  
 
Now we are ready to rewrite the integral,
 
Now we are ready to rewrite the integral,
  
−
:<big><math>\int\frac{2x}{x^2+3}dx=\int\frac{1}{u}du</math></big>
+
:<math>\int\frac{2x}{x^2+3}dx=\int\frac{1}{u}du</math>
  
−
We can rewrite the integral this way due to the substitution of the x terms with the u terms.
+
We can rewrite the integral this way due to the substitution of the ''x'' terms with the ''u'' terms.
  
−
Now we can solve the integral in terms of u.
+
Now we can solve the integral in terms of ''u''.
  
−
:<big><math>\int\frac{1}{u}du=ln|u|+c</math></big>
+
:<math>\int\frac{1}{u}du=ln|u|+c</math>
  
−
Now we replace u with the term :<big><math>x^2+3</math></big> to get,
+
Now we replace ''u'' with the term ''x''<sup>2</sup>+3 to get,
  
−
:<big><math>ln|x^2+3|+c</math></big>
+
:<math>\ln|x^2+3|+c</math>
  
−
We can check this by taking the derivative of :<big><math>ln|x^2+3|</math></big>,
+
We can check this by taking the derivative of <math display="inline">\ln|x^2+3|</math>,
  
−
:<big><math>\frac{d}{dx}ln|x^2+3|=\left (\frac{1}{x^2+3} \right)(2x)=\frac{2x}{x^2+3}</math></big>
+
:<math>\frac{d}{dx}\ln|x^2+3|=\left (\frac{1}{x^2+3} \right)(2x)=\frac{2x}{x^2+3}</math>
  
 
===Reverse Chain Rule===
 
===Reverse Chain Rule===
Line 82: Line 82:
 
</math>
 
</math>
  
−
This means that if a function can be recognised in the form f'(x)g'(f(x)), then it can be integrated almost immeadiately. As an example, consider the function:
+
This means that if a function can be recognised in the form f'(x)g'(f(x)), then it can be integrated almost immediately. As an example, consider the function:
  
 
:<math>
 
:<math>
Line 101: Line 101:
 
Given an integral  
 
Given an integral  
  
−
:<big><math>\int\frac{1}{\sqrt{9-x^2}}dx</math></big>
+
:<math>\int\frac{1}{\sqrt{9-x^2}}dx</math>
  
 
By looking at the radical we can determine that it represents the base of a right triangle by understanding the [[Pythagorean theorem]].
 
By looking at the radical we can determine that it represents the base of a right triangle by understanding the [[Pythagorean theorem]].
−
 
+
:<math>\sqrt{9-x^2}=3+x</math>
−
:<big><math>\sqrt{9-x^2}=3+x</math></big> where 3 is the hypotenuse and x is the height of the triangle.
+
where 3 is the hypotenuse and ''x'' is the height of the triangle.
−
This allows us to rewrite the expression to :<big><math>sin\theta=\frac{x}{3}</math></big>. This allows us to substitute x with :<big><math>3sin\theta</math></big>.   
+
This allows us to rewrite the expression to <math display="inline">\sin\theta=\frac{x}{3}</math>. This allows us to substitute ''x'' with <math display="inline">3\sin\theta</math>.   
 
Now to do the substitution
 
Now to do the substitution
−
:<big><math>9-x^2=9-(3sin\theta )^2</math></big>
+
:<math>9-x^2=9-(3\sin\theta )^2</math>
−
:<big><math>9-(3sin\theta )^2=9-9sin^2\theta </math></big>
+
:<math>9-(3\sin\theta )^2=9-9\sin^2\theta </math>
−
:<big><math>9-9sin^2\theta=9(1- sin^2\theta) </math></big> 
+
:<math>9-9\sin^2\theta=9(1- \sin^2\theta) </math>
 
And by use of trigonometric identities we know that  
 
And by use of trigonometric identities we know that  
−
:<big><math>1- sin^2\theta=cos^2\theta </math></big>
+
:<math>1- \sin^2\theta=\cos^2\theta </math>
−
:<big><math>9(1- sin^2\theta)=9cos^2\theta </math></big>  
+
:<math>9(1- \sin^2\theta)=9\cos^2\theta </math>
 
Therefore,
 
Therefore,
−
:<big><math>\sqrt{9-x^2}=3cos\theta </math></big>
+
:<math>\sqrt{9-x^2}=3\cos\theta </math>
−
We are not done yet, we must also take the derivative of :<big><math>3sin\theta</math></big>
+
We are not done yet, we must also take the derivative of <math display="inline">3\sin\theta</math>
−
:<big><math>\frac{dx}{d\theta}3sin\theta=3cos\theta </math></big>  
+
:<math>\frac{dx}{d\theta} 3\sin\theta=3\cos\theta </math>
−
By partial derivatives we move the :<big><math>{d\theta}</math></big> over.
+
By partial derivatives we move the <math display="inline">d\theta</math> over.
−
:<big><math>dx=3cos\theta d\theta </math></big>
+
:<math>dx=3\cos\theta d\theta </math>
  
 
Now we are ready to rewrite our integral.
 
Now we are ready to rewrite our integral.
  
−
:<big><math>\int\frac{1}{\sqrt{9-x^2}}dx=\int\frac{3cos\theta}{3cos\theta}d\theta=\int d\theta=\theta+c</math></big>
+
:<math>\int\frac{1}{\sqrt{9-x^2}}dx=\int\frac{3\cos\theta}{3\cos\theta}d\theta=\int d\theta=\theta+c</math>
−
 
+
−
From our trigonometric expression :<big><math>x=3sin\theta</math></big> we can see that
+
−
:<big><math>\theta=sin^{-1}\left(\frac{x}{3}\right)+c</math></big> giving us the final solution.
+
  
−
:<big><math>\int\frac{1}{\sqrt{9-x^2}}dx=sin^{-1}\left(\frac{x}{3}\right)+c </math></big>
+
From our trigonometric expression <math display="inline">x=3\sin\theta</math> we can see that
 +
:<math>\theta=\sin^{-1}\left(\frac{x}{3}\right)+c</math>
 +
giving us the final solution.
 +
:<math>\int\frac{1}{\sqrt{9-x^2}}dx=\sin^{-1}\left(\frac{x}{3}\right)+c </math>
  
 
== Other methods of integration ==
 
== Other methods of integration ==
Line 145: Line 145:
 
*[[Calculus]]
 
*[[Calculus]]
 
*[[Integration]]
 
*[[Integration]]
 +
*[[Table of Indefinite Integrals]]
  
 
==External links==
 
==External links==

Latest revision as of 21:36, October 15, 2020

This article/section deals with mathematical concepts appropriate for late high school or early college.

This article details several methods of integration for advanced high school or early university student, each with an example.

Estimation

There are various methods of estimating integrals. This is particularly useful if the rule for integrating is unknown or extremely complicated, as in the case of . The primary method of estimation is the Riemann integral.


Another major method, known as Simpson's rule uses the Riemann integral. Instead of using linear estimations, Simpson's rule allows for the use of parabolas or other higher order expressions to estimate integrals.

For a more detailed treatment, see Simpson's rule.

Integration by Parts

For a more detailed treatment, see Integration by parts.
Integration by parts is a special technique to facilitate the integration of the product of two functions that otherwise lack an obvious integral. This technique can be proven with the product rule.

The rule for integration by parts is stated as follows:

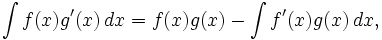
or

This rule is often useful when one function is a power of x and the other function is a trigonometric function or e raised to a power of x.

Note that it may be necessary to repeat the integration by parts several times, one for each power of x.

Partial Fractions

For a more detailed treatment, see Partial fractions in integration.
Integration by partial fractions is a technique to facilitate the integration of a rational expression by partial fraction decomposition.

Given an integral


where 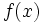and are both polynomials, integration by partial fractions shows how to separate the problem into multiple integrals before integrating.

Algebraic Substitution

Integration by Algebraic Substitution is a technique to facilitate the integration of a rational expression by substituting a more complicated expression with a variable.

Given an integral

We can substitute the term x2+3 with a u. Giving us

We then take the derivative of u with respect to x,

We then set the terms equal to du,

Now we are ready to rewrite the integral,

We can rewrite the integral this way due to the substitution of the x terms with the u terms.

Now we can solve the integral in terms of u.

Now we replace u with the term x2+3 to get,

We can check this by taking the derivative of ,

Reverse Chain Rule

The reverse chain rule is a trick for integration by substitution without having to do all the steps involved with integration by substitution. It uses a reversed form of the chain rule in differentiation to integrate functions of the form f'(x)g'(f(x)), where f and g are two functions and f'(x) is the derivative of f(x). From the chain rule, which states:

Integrating both sides produces the reverse chain rule:

This means that if a function can be recognised in the form f'(x)g'(f(x)), then it can be integrated almost immediately. As an example, consider the function:

Comparing to the above, f(x)=x2, f'(x)=2x and g'(x) is represented by a cosine. All wee need to do is know the integral of a cosine is sine so g(x) is sine. Therefore:

If the first part of the function is f'(x) multiplied by a constant, then this constant can be taken out of the integral so that it the integral is of the form f'(x)g'(f(x)). This method can also be applied to the fraction example above.

Trigonometric Substitution

Integration by Trigonometric Substitution is a technique to facilitate the integration of a rational expression by substituting a more complicated radical expression with a trigonometric expression.

Given an integral

By looking at the radical we can determine that it represents the base of a right triangle by understanding the Pythagorean theorem.

where 3 is the hypotenuse and x is the height of the triangle. This allows us to rewrite the expression to . This allows us to substitute x with . Now to do the substitution

And by use of trigonometric identities we know that

Therefore,

We are not done yet, we must also take the derivative of

By partial derivatives we move the over.

Now we are ready to rewrite our integral.

From our trigonometric expression we can see that

giving us the final solution.

Other methods of integration

The primary methods of integration include:

See also

External links

Retrieved from "https://conservapedia.com/index.php?title=Methods_of_integration&oldid=1696040"