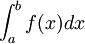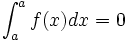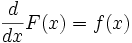Difference between revisions of "Integral"
(sp: definite integral) |
|||
| Line 70: | Line 70: | ||
==Lebesgue Integral== | ==Lebesgue Integral== | ||
| − | The Lebesgue integral is usually introduced in late university or early postgraduate mathematics. It is naively described as rotating the Reimann integral, in that it is the range instead of the domain that is partitioned. An understanding of [[measure theory]] is required to understand this technique. | + | The Lebesgue integral is usually introduced in late university or early postgraduate mathematics. It is naively described as rotating the Reimann integral, in that it is the range instead of the domain that is partitioned. An understanding of [[measure theory]] is required to understand this technique. Lebesgue integration is not taught in most religious schools, since its ability to integrate over almost any function and domain is deemed to be part of a '''liberal''' agenda to make integration "too accepting." |
==See Also== | ==See Also== | ||
Revision as of 19:26, March 2, 2009
|
This article/section deals with mathematical concepts appropriate for late high school or early college. |
An integral is a mathematical construction used in calculus to represent the area of a region in a plane bounded by the graph of a function in one real variable. Definite integrals use the following notation:
where a and b represent the lower and upper bounds of the interval being integrated over, f(x) represents the function being integrated (the integrand), and dx represents a dummy variable given various definitions, depending on the context of the integral.
Contents
Integration
Integration is the inverse function of the derivative and the two notions are related by the Fundamental Theorem of Calculus.
The concept of integration can be extended to functions in more than one real variable, as well as functions defined over the complex numbers.
Integration has many physical applications. The indefinite integral of an acceleration function with respect to time gives the velocity function defined to within a constant, while the definite integral of an acceleration function with respect to time gives the change in velocity between the upper and lower limits of integration. Likewise, the indefinite integral of a time function of velocity with respect to time gives the position function defined to within a constant, and the definite integral of this velocity function will give the change in position between the two limits of integration.
Methods of Integration
For a more detailed treatment, see Methods of integration.
There are many different ways to integrate functions. Sometimes, when it is impossible to directly integrate a function, an approximation is used, such as the Riemann integral. Or, there may be a process to integrate the function using a rule, such as with Integration by parts.
Types of Integrals
There are two types of integrals. Definite integrals are integrals that are evaluated over limits of integration. Indefinite integrals are not evaluated over limits of integration. Evaluating an indefinite integral yields the antiderivative of the integrand plus a constant of integration.
Properties of integrals
Intergation has the following properties[1]
Additive Distribution
If an integral contains two functions added together, it may be rewritten as two separate integrals, each containing one function.
Constant Multiplicative Distribution
If an integral contains a function multiplied by a constant, it may be rewritten as the constant times the integral of the function.
Area
Any integral that contains the same upper and lower bounds is equal to zero.
Separation
An integral may be rewritten as the sum of two integrals with adjacent bounds.
, 
Additive Inversion
Any integral is equal to the additive inverse of the same integral with reversed upper and lower bounds.
Antiderivative vs Integration
There are important differences between the anti-derivative and integration. An anti-derivative of a function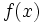 
is a function 
such that,
The integral of a function can be evaluated using its antiderivative,
This works for the kind of functions encountered in late high school and early university mathematics. It is, however, an incomplete method. For example one cannot write the anti-derivative of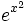 
in terms of familiar functions (such as trigonometric functions, exponentials, and logarithms) and function operations.
Riemann integral
For a more detailed treatment, see Riemann Integral.
As a geometric interpretation of the integral of the area under a curve, the Riemann integral consists of dividing the area under the curve of the function into slices. The domain of the function is partioned into N segments of width 
. The height of the segment is dependent on which side of the rectangle is taken. The lower sum takes the lower side of the rectangle, the upper sum the higher side of the rectangle. In the limit of 
these two series become the integral. If they approach the same value then the integral exists, otherwise it is undefined.
Simpson's Rule
For a more detailed treatment, see Simpson's rule.
Simpson's Rule is an extension of the Riemann integral. Instead of using shapes such as rectangles or trapezoids, Simpson's Rule allows for the use of parabolas or other higher order polynomials to approximate integrals.
Lebesgue Integral
The Lebesgue integral is usually introduced in late university or early postgraduate mathematics. It is naively described as rotating the Reimann integral, in that it is the range instead of the domain that is partitioned. An understanding of measure theory is required to understand this technique. Lebesgue integration is not taught in most religious schools, since its ability to integrate over almost any function and domain is deemed to be part of a liberal agenda to make integration "too accepting."
